(Please see the English Version)
Im Folgenden eine hoffentlich wohldosierte (??)
Prise Physik über die akustischen Phänomene der vorgestellten
Drachen-Musikinstrumente.
Siehe auch eine schöne
Seite über animierte akustische Effekte...

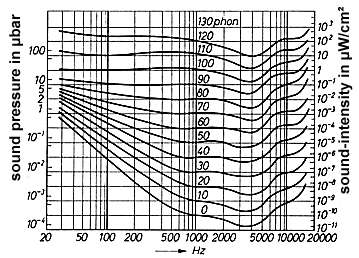
Das menschliche Ohr hört im Bereich von 16Hz bis ca. 20.000Hz, je jünger, desto höher. Aus dem obigen Diagramm ist zu erkennen, daß die größte Empfindlichkeit bei ca. 3000Hz bis 4000Hz liegt. Für Töne, die um diesen Bereich herum liegen, ist die kleinste Lautstärke nötig um gehört zu werden. Um den Faktor 107 größere Lautstärken sind bei sehr tiefen Tönen erforderlich; aber auch bei hohen Frequenzen nimmt die Empfindlichkeit des Ohres ab.
Damit gilt für alle Aeolsinstrumente, daß die Frequenzen von 1000 bis ca. 5000 Hz am besten gehört werden, für diese Frequenzen also die vergleichsweise geringsten Lautstärken erfoderlich sind um, wie bei Drachen-Musikinstrumenten, sehr weit gehört zu werden.
Die einzelnen Instrumenten-Typen:
Flöten/ Pfeifen allgemein
Wie erzeugen Pfeifen eigentlich einen Ton? In Anlehnung an Meyer's Konversationslexikon von anno 1905 geht das etwa so:
Bei den sog. Lippenpfeifen (und dazu
zählen alle Drachen-"Äolsflöten", wie auch Blockflöten
etc.) wird der durch den Pfeifenfuß (= Mundstück) eintretende
Luftstrom durch eine schmale Spalte (=Kernspalte; sowohl das
Mundstück als auch die Kernspalte erübrigen sich bei den
Drachenflöten, da via naturalis bereits eine laminare Anströmung
vorliegt, die nicht erst durch die Kernspalte erzeugt werden muß...)
gegen die scharfe Kante des Aufschnitts (Oberlabium = "Anströmkante")
getrieben, die ihn teilt und einen Teil des Luftstroms in den
Pfeifenkörper eintreten läßt, während der andere außen
vorbeiströmt. Durch die eintretende Luft wird die innen befindliche
Luft stark elastisch verdichtet (also ein Überdruck erzeugt), so daß
sie anschließend zurückfedernd den leicht ablenkbaren, außen
vorbeiströmenden Luftstrom ganz nach außen ablenkt. Nach dem
Venturiprinzip wird darauf durch den außen vorbeiströmenden
Luftstrom ein Teil der Luft in der Pfeife mit herausgesogen, so daß
nunmehr eine leichte Verdünnung (Unterdruck) in der Pfeife entsteht,
welche dann wiederum einen Teil des außen vorbeiströmenden
Luftstroms in's Flöteninnere lenkt. Dann geht's wieder von vorne
los; Überdruck-Unterdruck-Überdruck... und so weiter...ab einer
Frequenz von 16Hz (=16 mal Überdruck/ Unterdruck pro Sekunde)
entsteht ein für's menschliche Ohr hörbarer Ton, die Hör-Obergrenze
liegt bei etwa 20,000Hz.
So erzeugt also ein sich rhythmisch
abwechselnder Überdruck und Unterdruck den hörbaren Schall.
Hier die lasergestützte
graphische Animation (Laser Doppler Anemometer) des
Einschwingvorgangs an einer Orgelpfeife von der schönen
Seite des Orgelbauers Reiner Janke! Gut ist das aus der
Kernspalte austretende, für die Tonbildung verantwortliche Luftblatt
zu erkennen, welches hin und her schwingt.
Schauen Sie unbedingt
auf diese Seite Visualisierungsmethode;
besser kann man die Vorgänge kaum darstellen...
Siehe auch die schöne Seite (!) http://230nsc1.phy-astr.gsu.edu/hbase/music/edge.html über die Tonbildung am Schall-Loch.
Bedingt durch diese Über- Unterdruckerscheinungen in dieser sog "gedackten", geschlossenen Pfeife wird auch erklärt, daß eine Pfeife, die im Körper Undichtigkeiten, also Löcher, Risse etc. aufweist, umso schlechter klingt, je mehr Luft durch diese Leckagen strömen kann. Je größer das Leck, desto mehr Luft kann dadurch in der Überdruckphase entweichen/ in der Unterdruckphase eintreten und desto mehr werden diese für die Schallerzeugung essentiellen Phasen gedämpft. Damit das in der Pfeife eingeschlossene Luftvolumen zum Schwingen/ tönen kommt, muß das Schall-Loch (bei dem "gedackten/ hubischen Pfeifentyp)die einzige Öffnung sein , wo die Luft "Arbeit verrichtet"; denn nur dort macht's ja Sinn, sprich Musik. Dies gilt für die hier beschriebenen Drachenflöten.
Natürlich ist es möglich, auch offene Drachenflöten zu bauen. Ähnlich denen einer Kirchenorgel. Man muß aber bedenken, daß die offene Flöte um die gleiche Tonhöhe/ Frequenz zu erzeugen, doppelt so lang sein muß, wie sog. "gedackte", also geschlossene Flöten, zu denen die traditionellen Drachenflöten gehören. Und doppelte Länge bedeutet eben auch verdoppeltes Gewicht; immer ein Problem in der Luft; eben auch bei Drachen...
Noch ein Wort zu
den Drachen-Flöten:
Durch gleichzeitiges
Ertönen zweier baugleicher Pfeifen gleicher Frequenz und Lautstärke
ist unabhängig von der Ausgangslautstärke ein Lautstärkezuwachs
von lediglich 3 Phon erreichbar!
Der bessere
Weg um die empfundene (NICHT die physikalische,
gemessene!) Lautstärke zu
erhöhen ist die Hinzufügung von harmonischen Obertönen;
beispielsweise Terzen, Quinten, Oktaven oder Duodezimen etc.,
genau wie bei einer Orgel...
Eine weitere Möglichkeit der Verbesserung
der Vernehmbarkeit von Drachenpfeifen ist die Erzeugung von
Schwebungen (Effekt: Ton wird abwechselnd lauter und leiser)
durch geringes gegeneinander Verstimmen zweier
Pfeifen gleicher Tonhöhe.
Bei gleicher physikalische Schallstärke werden
Töne um 3000-4000 Hertz
von unserem Ohr als am lautesten empfunden. Extrem
hohe oder tiefe Töne benötigen ein Vielfaches an physikalischer
Schallstärke (...und damit Baugröße!) um als gleich laut
empfunden/ gehört zu werden!
Werden Pfeifen
in zu geringem räumlichem Abstand "face en face"
zueinander positioniert, kann dies zu Schallauslöschung führen,
da sich dann die Pfeifen gegenseitig zu 180° phasenverschobener
Tonbildung anregen.
Man sollte darauf achten, daß die
Flötenöffnungen/ Schall-Loch
möglichst dem Zuhörer zugewandt sind um den besten Abstrahleffekt/
Hörbarkeit zu erreichen.
Bei den "normalen" Pfeifen ist der Durchmesser sehr viel kleiner als die Länge; z.B.Blockflöte, Panflöte etc. Die Pfeifendicke kann deshalb zur Frequenzberechnung gegenüber der Länge vernachlässigt werden (beinahe, spielt eine Rolle für die Klangfarbe, also die Obertöne!). Dieses Verfahren ist allerdings nicht mehr zulässig, wenn die Pfeife nach allen drei Dimensionen gleichmäßig ausgebreitet ist. Man spricht dann von einer kubischen Pfeife, zu denen fast alle hier vorgestellten Drachenmusikinstrumente vom Flötentyp zählen (außer der vietnamesischen/ chinesischen CaÏ-Sao, da haben die Einzelflöten eine größere Länge als Durchmesser). Die "Idealform" der kubischen Pfeife ist die Kugel. Bei dieser schwingt das eingeschlossene Luftvolumen praktisch obertonfrei, nur der Grundton wird erzeugt.
Dessen Frequenz hängt nur vom schwingenden Luftvolumen und dem Schall-Lochquerschnitt ab (s.u.).
Wegen dieser Freiheit von Obertönen wurden deshalb früher analog
zu den kubischen Pfeifen kugelförmige Resonatoren zur Analyse von
zusammengesetzten Schallen/ Geräuschen benutzt. Der berühmte Arzt
und Naturforscher Hermann
v. Helmholtz (1821-1894) (siehe
"Die Lehre von den Tonempfindungen...") erfand die
nach ihm benannten Kugelresonatoren
(= auf eine bestimmte Tonfrequenz abgestimmte, einfache Glas-
oder Metallkugeln, mit einer Öffnung. Verhältnis Öffnung/
Volumen s.unten), bei denen das eingeschlossene Luftvolumen
weitgehend obertonfrei nur in der Grundfrequenz schwingt.
Erklingt in der Nähe ein Ton in der gleichen Frequenz, welche mit
der Frequenz des eingeschlossenen Luftvolumens des Resonators
übereinstimmt, so beginnt der Resonator infolge von
Resonanzerscheinungen mitzuschwingen und beginnt selbst zu tönen.
Auf andere, "fremde" Frequenzen spricht er nicht an. Wenn
man nun einen zusammengesetzten Schall analysieren möchte, steckt
man sich nacheinander verschieden abgestimmte Helmholtz-Resonatoren
in's Ohr und hört immer dann einen Resonanz-Ton, wenn der
entsprechende Teilton im Schallgemisch enthalten ist. Aus der
empfundenen Lautstärke kann man auf die Stärke der Teiltöne
schließen. Damit gelangen Helmholtz damals aus heutiger Sicht
erstaunlich exakte Schallanalysen.
Siehe Helmholtzresonatoren
Flaschenform
und Kugelform/
"Kondomform" und nochmals Kugelresonatoren.
Eine praktische Anwendung ist die gezielte Schallverstärkung beispielsweise in antiken Theatern oder an Glockentürmen; hier der "torre das cabacas" (Kürbisturm) in Santarém in Portugal. Die kürbisähnlichen Gefäße verstärken die Glockentöne.
Nun kommt unweigerlich die Frage der Berechnung...
Die Resonanzfrequenz (=Flöten-Ton-Frequenz)
Bei rundem Schall-Loch:
f = ((r x c)/2) x Wurzel[ 1 / (V x Pi x (d + (1,7 x r )))]
Bei beliebiger Form des Schall-Loches:
f = ( c / (2 x Pi)) x Wurzel[A / (V x ( d + SQR( A )))]
c = Schallgeschwindigkeit in
cm/s
f = Frequenz des Resonators in
Hz
d = Wanddicke des Resonators an der
Öffnung in cm
r = Radius des
Schall-Loches in cm
V = Volumen des
Resonators in cm3
A =
Projezierte Fläche des Schall-Loches in cm2
Pi
= 3,14159265359
Helmholtz gibt in seiner "Lehre
von den Tonempfindungen..." auf den Seiten 600-603
(Beilage I.) die folgenden Formeln für die Resonanzfrequenz seiner
Kugelresonatoren an (Wobei die Kugelöffnung, die ins Ohr eingelegt
wird, vernachlässigt werden kann):
|
|
|
a =
Schallgeschwindigkeit |
oder
|
|
|
für kugelförmigen Resonator |
Die Volumenberechnung des Resonators
Bei rundem Schall-Loch:
V = ((r2 x c2) / (4 x Pi x f2 x (d + Wurzel(A)))
Bei Schall-Loch von beliebiger Form:
V = (A x c2) / 4 x Pi2 x f2 x (d + Wurzel( A ))
c = Schallgeschwindigkeit in cm/s
f
= Frequenz des Resonators in Hz
d
= Wanddicke des Resonators an der Öffnung in cm
r
= Radius des Schall-Loches in cm
V =
Volumen des Resonators in cm3
A
= Projezierte Fläche des Schall-Loches in cm2
Pi
= 3,14159265359
Zu weiteren Details siehe die Seiten von Dr.Godfried-Willem Raes (in niederländisch)
Wenn Sie also jetzt wissen möchten, wie die Pfeifen
auf dem über Ihnen fliegenden Drachen gestimmt sind, könnten
Sie Helmholtz-Resonatoren nehmen und damit eine "Ferndiagnose"
stellen.....
Die Pfeifen benötigen in Abhängigkeit von ihrer
Bauweise eine Windgeschwindigkeit (bis sie ansprechen) von 20-30Kmh
das entspricht einer Geschwindigkeit von etwa 5m pro
Sekunde.
Umrechnungsformel: (m/sec. mal 3,6) +10% = Kmh
Das
heißt, wenn man als Windspiel zum Beispiel eine Windmühle baut und
die Flöten auf die Flügelspitzen setzt muß der Windraddurchmesser
etwa 160cm betragen wenn die Umdrehungsfrequenz bei 1Hz liegt!
Alles zu theoretisch? Hier sind Schwingungen zum Anschauen und damit Spielen; Sie werden staunen...
(Siehe auch "Verbundsaite" des kamodschanischen "EK", die Rotations-Schwingungen ausführen, also sich nicht wie die nachfolgenden "normalen" Saiten unserer bekannten Musikinstrumente verhalten!)
Schwingende Saiten (siehe Schwingungen)sind das zweidimensionale Gegenstück zu schwingenden Membranen. Saiten besitzen keine Eigenelastizität, weswegen sie an beiden Enden eingespannt werden müssen um überhaupt elastische Schwingungen ausführen zu können. Dabei sind von besonderer Bedeutung die Biegungsschwingungen (oder Quer-, Transversalschwingungen), die bei den Saiteninstrumenten ausgenutzt werden. Saiten können durch Schlagen (z.B.Klavier), Zupfen (z.B.Gitarre) oder durch Streichen mit einem Bogen (z.B.Geige) zum Schwingen erregt werden. Bei den Äolsharfen, Drachen-Musikbogen etc. regt der vorbeiströmende Wind die Saiten an.
Dieser Effekt kann an Überlandleitungen fatale Folgen haben. Siehe die super Seite über das "Galoping" Phänomen - nichts anderes als eine Riesen Äolsharfe...
Der genaue Mechanismus, WIE dies
geschieht, ist inzwischen recht gut erforscht. Die ersten Arbeiten
hierüber machte 1878 in Würzburg Vincenc Strouhal (siehe
Originaltexte aus seiner Arbeit) in seiner
Habilitationsschrift "Über eine
besondere Art der Tonerregung", in der er Reibungstöne
der Luft an Hindernissen (siehe
Literatur hierüber) beschrieb. Eine bedeutende Rolle spielen
bei der Saitenanregung durch den Wind die von Kármán'schen
Wirbelbildungen (abhängig vom Durchmesser und der
Windgeschwindigkeit) im Lee der Saite (siehe weitere
Literaturhinweise). Durch die
alternierenden rhythmischen Wirbelablösungen (und deren
alternierenden "Saugeffekt") auf beiden Seiten der Saite in
90° zum anströmenden Wind, wird die Saite selbst zu Schwingungen
angeregt; wenn die Resonanzfrequenz der Saite erreicht wird, fängt
sie an laut zu tönen.. Auf diese Weise (Flatterschwingungen) wurden
sogar Brücken (Tacoma Narrows Bridge) zum Einsturz gebracht!!!
(Siehe
video! 700K). Ein Videofilm
über das Unglück mit 13,5min. Länge ist im IWF zu
entleihen. Siehe gute
Erklärung des Unglücks...
|
|
|
Schema einer Flatterschwingung entlang der
Flachsaite gesehen |
|
|
|
...und so werden runde Stahlseile zu
schwingenden Bandsaiten... |
Hier sehen Sie die Wirbelbildung an einer Rindsaite als
Animation (Quelle: Die schöne Seite von Cesareo
de La Rosa Siqueira): .
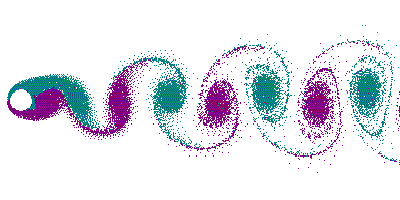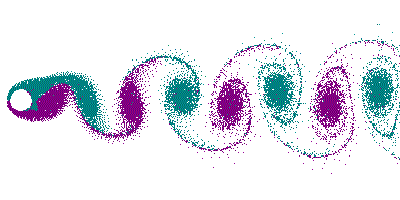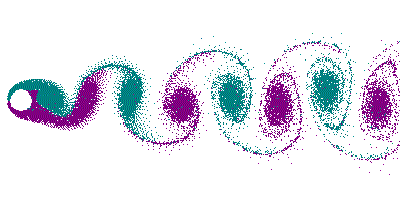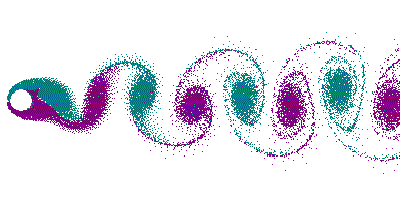
Und so hört sich eine solche Wirbelstraße an (die Aufnahme entstand an meiner Zimmertür als draußen ein Gewitter tobte...
Siehe Lebenslauf von v. Kármán...
Auch in der freien Natur z.B. im Lee von Inseln (auf der Seite von T.J.Praisner) sind sie zu sehen. Ein Kuriosum: Das Schwingen von vereisten Leitungen in der Antarktis bei fast völliger Windstille siehe Alaska Science Forum . Funktioniert alles nach demselben Prinzip. Schöne Simulationen auch bei http://www.swcp.com/itsc/movies/acel.mpg
|
|
|
Entwicklung der Umströmung eines Zylinders |
...und noch ein praktisches Experiment in der Badewanne...
Ein besonderes Merkmal ist, dass die Abstände der einzelnen
Wirbel – und damit auch die Struktur der gesamten Wirbelstraße –
bei unverändertem Widerstandskörper gleich bleiben, unabhängig von
der Strömungsgeschwindigkeit. Dies hat zur Folge, dass mit
steigender Strömungsgeschwindigkeit sich die Flüssigkeit oder das
Gas schneller vom Widerstandskörper ablösen und die Wirbel in
rascherer zeitlicher Abfolge, aber weiterhin in konstantem Abstand,
entstehen.
Hier nochmals ein anderes animiertes Abbild einer
schwingenden Saite und ihrer
Umströmung:
http://www2.icfd.co.jp/examples/movingcylinder1/cyl12.html
|
...und noch ein kleines Windharfen-Spezial: Nach dem sehr lesenswerten Artikel von Erich Bäuerle aus Äolsharfen: Der Wind als Musikant seien hier für besonders Interessierte noch spezielle Formeln zum Windharfenbau / Saitenbestückung aufgeführt:
|
Zurück zu den Saiten:
Normalerweise haben Saiten eine sehr
kleine projezierte Fläche, die sie dem vorbeiströmenden Wind
zum Anregen der Schwingung bieten können. Deshalb gibt es kaum
Drachen Musikinstrumente mit runden Saiten (mir ist nur der
chinesische Drachen-Summer Feng-Qin
bekannt), die zudem recht leise sind wegen der kleinen
Abstrahlfläche. Zur Erleichterung der Ansprechbarkeit der Saiten und
gleichzeitiger Erhöhung der Lautstärke muß man folglich diese
projezierte Fläche vergrößern. Dies geschieht bei den
Drachenmusikinstrumenten praktisch dadurch, daß man entweder
bandförmige Saiten (z.B. chinesische Yao-Ch'in,
kambodschanischer Èk, japanischer Unari; chinesische Fêng-Chêng;
siehe Instrumente vom Äolsharfen-Typ...)
verwendet oder aber als Spezialfall einen Teil einer an sich runden
Saite mit Papier beklebt (z.B. Bermuda-Summer).
Dadurch erreicht man, daß die Saiten bereits bei sehr geringen Windgeschwindigkeiten zu klingen/ anzusprechen beginnen.
Bei der Anbringung von mehreren kurzen bandförmigen
Saiten darauf achten, daß sie
... nicht in sich verdreht sind; z.B. beim "Unari". Im Extremfall, wenn dieser "Twist" mehr als etwa 45°-90° beträgt, wird die Saite stumm bleiben oder zumindest eine wesentlich größere Windgeschwindigkeit benötigen, bis sie anspricht.
Andererseits klingen nach meiner Erfahrung flache, lange Stahlsaiten (Bandstahl, 20-50m Länge) erst dann, wenn sie einen Twist haben Über die Anzahl der so vorgegebenen Schwingungsknoten/ -bäuche kann die Klangfarbe/ Anzahl der Obertöne mitbestimmt werden... also probieren!
Wird eine Saite angezupft, so schwingt sie zunächst als Ganzes hin und her und erzeugt dadurch den Grundton; darüber hinaus schwingt sie jedoch auch in sich selbst immer so, daß an den eingespannten Enden stets Schwingungsknoten entstehen.
Wenn l die Länge der Saite ist, c die von der Saitenspannung abhängige Ausbreitungsgeschwindigkeit der Welle in der Saite, dann gilt für die Frequenz f der Schwingungen:
f = n·c / 2·l mit n = 1,2,3,...
Für n = 1 erhält man die Frequenz f 0 der Grundschwingung:
f 0 = c / 2·l
Die Frequenzen der Oberschwingungen (=Obertöne) ergeben sich, wenn man für n nacheinander die Zahlen 2, 3, 4,... einsetzt. Daran erkennt man aber, daß die Frequenzen der Obertöne ganzzahlige Vielfache der Grundfrequenz sind.
Die Saite erzeugt also harmonische Obertöne und damit einen Klang.
Bei schwingenden Membranen oder einseitig
eingespannten schwingenden Stäben sind die Obertöne
unharmonisch, d.i.keine ganzzahligen Vielfache des Grundtones.
Deshalb entsteht kein Klang, sondern ein Tongemisch, deshalb
sind Membranen und schwingende Platten für musikalische Zwecke nur
bedingt geeignet.
Es gibt eine allgemeine Formel für die Frequenz v in Abhängigkeit der Saitenlänge l, der spannenden Kraft K, der Querschnittsfläche F und der Dichte p des Saitenmaterials:
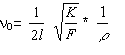
Oder etwas anders als Taylor'sche Formel, wobei f die Frequenz, L die Länge der Saite, P die Saitenspannung und m die Masse pro Längeneinheit der Saite ist.
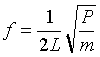
Wer's ganz genau wissen möchte, hier noch eine schöne Abhandlung über das Verhalten von Saiten. Abschnitt über aeolische Töne an Saiten ganz unten in diesem Artikel.
Saitenlänge und Tonhöhe
Noch was zum Verhältnis Saitenlänge/ Tonfrequenz. Die Saitenlänge sei gleich 1 und erzeuge den Ton C. Ausgehend von diesem Ton bei gegebener Saitenlänge findet man die nächstfolgenden Töne D, E... etc. durch Multiplikation der Saitenlänge 1 mit dem Faktor.....s.u. Dieses Verhältnis stimmt für alle Töne! Das Frequenzverhältnis ist entsprechend reziprok.
Die untenstehende Tabelle (eine Oktave, nach oben analog fortzusetzten) gilt für die "gleichschwebend= temperierte Stimmung".
Kammerton a'=435,00 Hz (Festlegung des
Referenztons durch eine internationale Konferenz in Wien im Jahre
1885).
|
Saitenlänge/ Verhältnis |
1 |
8/9 |
4/5 |
3/4 |
2/3 |
3/5 |
8/15 |
1/2 |
|
Musik.Bezeichnung |
C' |
D' |
E' |
F' |
G' |
A' |
H' |
C'' |
|
Frequenz (Hz) |
261.63 |
293.66 |
329.63 |
349.23 |
392.00 |
440.00 |
493.88 |
523.25 |
Nach Relf existiert in Bezug auf die Möglichkeit der Tonerzeugung durch Wind an Saiten eine Grenzgeschwindigkeit, die durch folgende Gleichung (empirisch) repräsentiert wird:
V*D/v
>=100
V= Windgeschwindigkeit, D=Drahtdurchmesser,
v=Viskosität des Mediums.
Wenn bei gegebenem Drahtdurchmesser die Gleichung weniger als (ungefähr) 100 ergibt, kommt es zu keiner Wirbelbildung (=Tonbildung) hinter dem Draht.
Und für Rechenfaule hier noch ein kleines Saiten-Kalkulationsprogramm zum Herunterladen auf der Seite http://www.massmedia.com/~mikeb/mando/stringcalc.html
Und noch ein nettes Saiten-Kalkulationsprogramm
Die Besonderheit:
Verbundsaite
beim kambodschanischen
"Ek"
Hören Sie zu Beginn ein Hörbeispiel des "Ek"-Musikbogens. Wohlgemerkt, es handelt sich wirklich nur um EINE EINZIGE Saite!!
Diese
Verbundsaite, die aus einem breiten, bandförmigen, relativ
verwindusngssteifen Mittelstück besteht, das beidseits mit mehreren
dünnen Fäden am zughörigen Bambusbogen befestigt ist, verhält
sich etwas anders als die vorher beschriebenen Band-Saiten. Sie
schwingt wie die diese in Transversalschwingungen UND
führt gleichzeitig eine Rotation mit alternierender
Rotationsrichtung sowie unterschiedlicher Geschwindigkeit um ihre
eigene Achse durch.
Schwingungsformen
siehe hier.
Die Anzahl der Schwingungsbäuche
bestimmt die Rotationsgeschwindigkeit, d.i. die Umdrehungen pro
Sekunde und diese wiederum bestimmt die Frequenz. Tiefer Ton =
wenig "Bäuche", hohe Frequenz = viele "Bäuche".
Die Frequenz ist abhängig von der Biegesteifigkeit der Saite und
ihrem Trägheitsmoment (also vom Gewicht pro Längeneinheit und von
der Saitenbreite); also je schwerer/ breiter im Verhältnis zur Länge
die Saite ist, desto langsamer rotiert sie und desto tiefer der Ton.
Zum Vertiefen des Tons (und zum Verlängern des Rotationszyklus)
kleben die Kambodschaner Bienenwachs an beide Enden des
Saiten-Mittelstücks und erhöhen dadurch das Drehmoment.
Die ideale Saite ist möglichst dünn und leicht (Masse) und dabei so flexibel wie möglich und darf so wenig wie möglich torquierbar sein.
Ausschlaggebend für die Lautstärke ist neben der Rotationsfrequenz (=Tonhöhe. Das menschliche Ohr hat sein Maximum um die 4000Hz) hauptsächlich die projezierte Fläche des Saiten-Mittelstücks. Je größer diese Schall-Abstrahl-Fläche, desto lauter der Ton. Es macht also Sinn, dieses Instrument größer und damit lauter zu bauen.
Zum Verändern der Rotations-Dauer, also des
einzelnen Rotationszyklus sind zusätzlich zum Drehmoment noch andere
Dinge ausschlaggebend:
Die Bogenspannung. Je gespannter der
Bogen, desto schneller der Zyklus.
Die Verdrehbarkeit der
Spannschnüre. Je mehr die Schnüre der Torsion Widerstand
entgegensetzen, desto schneller der Zyklus.
Ein meisterhaft gefertigter "Ek"-Bogen gibt sieben Töne ab.
Die Frequenzanalyse sieht beim "Èk" beispielsweise wie untenstehend aus. Zu sehen sind die unterschiedlichen Gipfel, die jeweils einem anderen Ton entsprechen. Auffällig ist die in etwa gleiche Lautstärke der einzelnen Töne und der gleichmäßige Abstand der Gipfel, gleichbedeutend mit einer harmonischen Abfolge der Töne ohne Dissonanzen. Dies bedingt den "Lied-artigen" Charakter der Tonfolge.
|
|
Hauptfrequenzen des "Èk". |
Möglichkeiten, ungewollt oder beabsichtigt, je nachdem...
Saiten sind prinzipiell schlechte Schallstrahler, dabei schneiden runde Saiten wesentlich schlechter ab (sie sind fast unhörbar), als bandförmige. Saiten-Musikinstrumente brauchen deshalb einen sogenannten Resonanzkörper oder Resonanzboden, der durch die Saitenschwingung zum Mitschwingen angeregt wird und infolge seiner großen Oberfläche als guter Abstrahler wirkt. Als Resonanzkörper/ Schallabstrahler wirkt beim Drachen die große Fläche des Drachengestells mit seiner (idealerweise...) Papierbespannung. Resonanzerscheinungen (=Eigenresonanz) mit großen Amplituden bei bestimmten Tönen sollten dabei allerdings nicht auftreten (z.B. Blechdosenklang). Unerwünschte Resonanzkatastrophen, wie z.B. das Zerreißen des Papiers auf dem mitschwingenden Drachen sind dann zumindest theoretisch denkbar.
Weitere Möglichkeiten zur Schallverstärkung sind das Anbringen von mehreren genau gleich gestimmten Saiten oder Pfeifen. Dieses Prinzip wird vor allem bei den chinesischen Nantong Drachenflöten, der CaÏ-Sao, der "Weinheimer-Querflöte" und der "Wind-Orgel" genutzt (siehe diese auf der Hauptseite).
Die Hauptmethode zur Schallverstärkung bei Windharfen/ Aeolsharfen besteht darin, den Resonanzkörper mittels dessen Verhältnis von Volumen zur projezierten Schall-Lochfläche auf den hauptsächlich auftretenden Saitenton abzustimmen. Untenstehend die Frequenzen, die via Klopfen an den Resonanzkörper erhalten wurden. Treffen die Harmonischen der Saiten auf diese Töne, so erklingen sie verstärkt.
|
|
|
Klopfton-Resonanz-Frequenzspektrum |
Ein wichtiger Aspekt mit dem sich schön spielen läßt sind sog. Schwebungen (siehe ein Beispiel auf http://www.monroeinstitute.com/programs/bbapplet.html). Dieser Effekt wird beispielsweise bei den Nantong Drachenflöten, sowie bei der "Windorgel" absichtlich erzeugt und trägt wesentlich zu deren Klangeffekt bei.
Zur Erzeugung einer Schwebung werden zwei Flöten / Saiten absichtlich ein ganz klein wenig unterschiedlich gestimmt, so daß sich die beiden Tonfrequenzen nur minimal voneinander unterscheiden.
Bei der Überlagerung von zwei Schwingungen mit nur geringem Frequenzunterschied ergibt sich als Resultierende eine Schwingung, deren Frequenz gleich dem arithmetischen Mittel (f1+f2)/2 der Frequenzen der beiden Teilschwingungen ist und deren Amplitude zwischen Null und einem Maximalwert mit der Schwingungsfrequenz fs = |f1-f2| schwankt. Für Schallwellen heißt das aber: Treffen zwei Schallwellen nahezu gleicher Frequenz zusammen, hört man statt zweier verschiedener Töne mit den Frequenzen f1 und f2 nur einen Ton der Frequenz (f1+f2)/2. Die Stärke dieses Tons schwankt mit der Schwebungsfrequenz fs = |f1-f2| zwischen einem Maximalwert und einem Minimalwert. Ist die Amplitude der beiden Schallwellen genau gleich, so ist der Minimalwert gleich Null, das heißt, wir hören einen Ton, der zwischen einem Maximalwert (mit doppelter Amplitude des Einzeltons) und absoluter Stille schwankt. Ist die Schwebungsfrequenz fs größer als 16 Hertz (= untere Hörschwelle des menschlichen Ohrs), so nimmt man nicht mehr die Lautstärkeschwankungen wahr, sondern hört die Schwebungserscheinung als selbständigen Ton.
Nebenbei: Analog funktioniert die "Vox Coelestis" auf der Kirchenorgel, bei der Töne erzeugt werden, für deren Pfeifen kein Platz (oder Geld...) da ist...Also ein Ton ohne die entsprechende, physisch vorhandene Pfeife.
Schwebungserscheinungen werden praktisch genutzt bei der Instrumentenstimmung. Zwei Saiten/ Pfeifen etc. sind auf genau den gleichen Ton gestimmt, wenn man bei deren gleichzeitigem Erklingen einen einzigen Ton gleichbleibender Stärke (also keine Schwebungen) hört.
Durch die Schwebungserscheinungen wird auch erklärt, daßt es eben doch Sinn macht, Lautsprecher zu bauen, die Frequenzen erzeugen können, die oberhalb der menschlichen Hörschwelle von 20.000 Hertz liegen. Die erzeugten Schwebungen liegen dann eben dann doch wieder im hörbaren Bereich...
Hier eine schöne Seite mit Klangbeispielen zu Schwebungen: http://www.phys.unsw.edu.au/jw/beats.html
Noch ein Wort zur besten Zeit, um die Drachen
Musikinstrumente in Aktion zu versetzten....
Im Königreich Annam,
dem heutigen Vietnam, war es Sitte der Eingeborenen, den eigenen
Gesang des Nachts von Musikdrachen begleiten zu lassen....(siehe
Artikel in französisch)
Am allerbesten geeignet ist die Nachtzeit und dies aus folgenden
Gründen:
Nachts herrschen sehr gleichmäßige Windverhältnisse,
da es dann keine von der Sonneneinstrahlung verursachte Thermiken
mehr gibt. Diese über erwärmten Flächen aufsteigenden Luftmassen
verursachen böigen Wind.
Am besten ist von Bergen abfließende
Luft im Herbst, Winter und Frühling bei sog.
"Strahlungswetterlagen" mit wolkenlosem Nachthimmel. Die
Luft fließt dann wie Öl und erzeugt Töne wie sonst nie...
Bei gleichbleibender Temperatur der Luft kann auch der Wind den Verlauf eines Schallstrahles ändern. Der mit dem Wind laufende Strahl krümmt sich nach unten, der gegen den Wind laufende Strahl jedoch nach oben. Deshalb sind bei starkem Wind gegen den Wind gerufene Worte nur auf kurze Distanz verständlich (mal ganz abgesehen von der Überlagerung durch das Geräusch, das durch den Wind selbst erzeugt wird). So kann die Reichweite eines Schallsignals auch durch den Wind bedeutend beeinflußt werden.
Um die Saiteninstrumente vom Typ der Aeolsharfe zum Klingen zu bringen, muß der Luftstrom die Saite möglichst auf ganzer Breite und möglichst gleichmäßig treffen. Verwirbelter Wind im Lee eines Baumes beispielsweise oder böiger Wind sind ungünstig. Der Ton braucht eine ganze Weile um sich zu "entwickeln". Oft spürt man vor dem Beginn eines Tones an der Saite zunächst ein Klopfen, das sich allmählich in der Frequenz erhöht, solange bis dann ein Ton hörbar wird. Dauert in der Regel einige (5-10) Sekunden!
Windkraft: http://www.meteo.physik.uni-muenchen.de/lehre/manuskripte/Wind.pdf
Die folgende Tabelle bezieht sich auf Windstärken
in 10m Höhe über dem Boden am Meer. Bei 4m Höhe kann man mit 20%
kleineren, bei 30m mit etwa 20% höheren Werten rechnen.
Je nach
Geländerauhigkeit muß bei 100 m Drachen-Höhe mit 40% höheren
Wertten gerechnet werden.
Die Windkraft steigt nicht linear,
sondern mit dem Quadrat der Windgeschwindigkeit!
Der Staudruck W (Wind-Druck auf eine ebene
Fläche quer zur Windrichtung) berechnet sich nach der Formel:
W
= 0.5 * (C * Rho * V2)
C
ist der von der Körperform abhängige Widerstandsbeiwert; Rho
die Luftdichte in Abhängigkeit von der Temperatur, V die
Windgeschwindigkeit. in m/s
Umrechnungsformel: (m/sec. mal 3,6) +10% = Kmh
|
Grad Beaufort (Bft.) |
Seemännische Bezeichnung |
Effekt im Gelände |
Meter/ Sekunde |
Stundenkilometer km/h |
Staudruck kg/qm |
|---|---|---|---|---|---|
|
0 |
still |
vollkommene Luftruhe, |
0-0,2 |
unter 1 |
0 |
|
Ab Stärke 1 |
leiser Zug |
Rauch steigt nicht ganz gerade empor, Blätter noch unbewegt |
0,3-1,5 |
1 bis 5 |
0-0,1 |
|
2 |
schwache Brise |
eben spürbar |
1,6-3,3 |
6 bis 11 |
0,2- 0,6 |
|
Ab
Bft.3 |
leichte Brise |
Blätter bewegen sich, |
3,4-5,4 |
12 bis 19 |
0,7- 1,8 |
|
4 |
mäßige Brise |
kleine Zweige bewegen sich, |
5,5-7,9 |
20 bis 28 |
1,9- 3,9 |
|
Ab Stärke 5 |
frische Brise |
größere Zweige bewegen sich, Wellenbildung |
8,0-0,7 |
29 bis 38 |
4,0- 7,2 |
|
6 |
starker Wind |
bewegt größere Zweige, |
10,8-13,8 |
39 bis 49 |
7,3- 11,9 |
|
7 |
steifer Wind |
bewegt schwächere Baumstämme, |
13,9-17,1 |
50 bis 61 |
12,0- 18,3 |
|
8 |
stürmischer Wind |
bewegt ganze Bäume |
17,2-20,7 |
62 bis 74 |
18,4- 26,8 |
|
9 |
Sturm |
Dachziegel und leichtere Gegenstände werden bewegt |
20,8-24,4 |
75 bis 88 |
26,9- 37,3 |
|
10 |
schwerer Sturm |
Bäume und leichte Bauten werden umgeworfen |
24,5-28,4 |
89 bis 102 |
37,4- 50,5 |
|
11 |
orkanartiger Sturm |
schwere Zerstörungen |
28,5-32,6 |
103 bis 117 |
50,6- 66,5 |
|
ab 12 |
Orkan |
Verwüstungen |
ab 32,7 |
ab 118 |
66,6 und mehr |
Aeolsharfen
hören bei ca. Windstärke 6 auf schön zu klingen - oder
überhaupt zu klingen. Wegen der unvermeidlichen
Turbulenzen...
Aeols-Flöten
können open end bis zu Orkan-Windstärke arbeiten...
Siehe schönes deutsches Buch über die Welt des Schalles...
Rechner für Helmholtz-Resonatoren
Immer noch nicht genug??? Dann besuchen Sie die Seiten der Georgia States University. Diese Seiten haben auf alles eine Antwort...
Alles über "Stimmungen" und ihre wohltemperierte Entwicklung...
A.Campanella's schöne Seite über Akustik - oder wußten Sie, daß es Sonolumineszenz gibt?
Fourier Series Applet zum Spielen...
Siehe auch Bücher von Fletcher und vor allem Spektrum der Wissenschaft über die Physik der Musikinstrumente.
Schöne Animationen akustischer Phänomene Animation courtesy of Dr. Dan Russell, Kettering University
Und wer zum Schluß noch wissen möchte, warum ein Drachen fliegt und überhaupt...
Anregungen, Kritik, Fragen......? ...dann
bitte Mail to
Kite Musical
Instruments!
gestaltet
und weiterentwickelt von
Uli Wahl, all rights reserved
(letzte
Änderungen vom 31.Januar 1999)
Zurück zur Hauptseite.
English Version follwing beneath....
In the following a hopefully well-dosed (?) pinch of physics on the acoustic phenomenons of the kite musical instruments presented by these pages.
What do we hear at all??

The human ear hears in a range of 16Hz up to ca. 20.000Hz, the younger the individuals, the higher the frequency which can be heard. The diagram shows, that the ear's highest sensibility is between ca. 3000Hz to 4000Hz. For tones in that range, the smallest possible volume is needed for being heard. Concerning tones of very low pitch, much higher volumes with a factor 107 are needed in order toe be heard; the same is with higher frequencies, where the sensibility of our ear is much lower, too.
So it is an important fact for all aeolian/ wind-powered instruments to be tuned (depending on the intended effect, however) on frequencies between 1000Hz up to ca. 5000 Hz in order to be heard best, or, in other words being heard in a distance as far as possible.
How can whistles generate a tone? Following the German Meyer's Encyclopedia of Conversation (Meyer's Konversationslexikon) from anno 1905 it's working like that:
When regarding the so called lip-whistles ( = all sorts of Kite-Flutes presented here) the airstream is entering in the so called "whistle's foot" (=conical bottom part of the organ pipe) and a narrow slit (=core slit at organ pipes) in order to make the airstream laminar before it enters the flute's "working parts" i.e. the sound generating part of the whistle in its sense. For the airstream on a kite is generally laminar there is no need of such entry parts (=no foot, no core slit) of a flute on a kite. The airstream now meets the sharp leeward edge of the sound hole, being divided there in two parts. The one part is entering the flute, compressing the enclosed air in the flute, thus generating an excess pressure onto the elastic air. The other part of the airstream meanwhile flows over the outside of the soundhole. The springy, compressed air now escapes from the interior of the flute through the sound hole, being inducted by the airstream flowing over the soundhole (Venturi-tube principle) , thus generating a lower pressure inside of the flute. The lower pressure will now force the airstream re-entering into the sound hole thus generating an excess pressure......and so on. Also see about edgetones and effects of different variations of the soundhole http://230nsc1.phy-astr.gsu.edu/hbase/music/edge.html.
The frequency (and also the accompanying harmonic tones) of how often the air-blade is vibrating back and forth depends on the whistle's length/ width and whether it is closed at its end or not.
Please have a look onto an infrared laser-based graphic animation (Laser Doppler Anemometer) of the transient effects at an organ-flute on the beautiful pages by the organ-builder Rainer Jank! Swinging back and forth, the "air-blade" is leaving the core-gap/ core-slit of the organ-flute's fipple, thus generating the sound in the organ flute.
On the same site the corresponding method of measuring/ visualizing these processes.
So a rhythmically alternating high/ low pressure (air acting like a metal spring) inside of the flute is generating the sound which can be heard.
When looking at these high/ low pressure phenomenons, it's explained, that a whistle will sound badly when there are even little holes/ fissures in their "body", where the air can escape or enter depending on the high/ low pressure phase. The kite whistle is the type of a "closed flute", so the soundhole has to be the only opening in the kite whistle.
It is possible, however, to build kite flutes as "open flutes" like in a church-organ. They function well; but for the same frequency, the open flute is double as long (=doubled weight!) than a closed flute. And on a kite in the air, additional weight is a problem...
Just a word
considering Kite-Whistles:
By simultaneous
sounding of two identical whistles of the same frequency and volume,
an increase of
loudness of only 3 Phone can be reached;
independent of the original loudness!
A better way to
increase the perceived loudness (NOT the physical one) is the
addition of harmonic tones like octaves, fifth or thirds.
Another possibility to
improve the audibility of kite whistles, is the generation of
interferences by slightly "mistuning" two whistles against
another.
Provided the
same physical (=measured) strength of sound, tones around 3000-4000
Hertz are perceived the best by the human ear.
Extremely high or low tones need many times more of physical
power to produce the same sensation/ effect of loudness for the
human ear.
When whistles
are located in a distance too near to another ("face to face"),
this can result in an extinction of sound, for
the whistles will induce one another to a phase displacement angle
of 180°, leading to an almost complete distortion of tone.
For producing the best radiation/ audibility effect, one should pay attention to direct the whistle's openings/ soundholes towards the audience, however.
Considering "normal" flutes, the diameter generally is much smaller than its length; for example Pan's flute, recorder flute etc. The diameter thus can (almost) be neglected when determining the tone. This calculation is not allowed when the whistle's measures are equal in all three dimensions. Then we speak of a so called cubic whistle; to this type belong all the kite whistles presented here (except of the Cai-Sao kite flute, here is the diameter smaller than it's length). The ideal form of the cubic flute is a sphere. In this case the enclosed air is vibrating without harmonic tones (overtones) at all. Only the fundamental tone (only one single frequency) is generated! The frequency depends only on the enclosed swinging volume and the area of the soundhole (see below).
Because of the absence of overtones in its sound, in analogy to cubic flutes resonators in bowl-shape were used for sound analysis in former times. The German physician and physicist Prof. Hermann v. Helmholtz (1821-1894) invented the spheric-resonators (= simple glass or metal-bowls with an opening, calibrated to a certain frequency. See article in German with b/w pictures named after him. The air enclosed in these special resonators has the property to vibrate in only one special frequency, the fundamental frequency; overtone-frequencies don't occur. When a tone of the same special frequency the resonator is tuned on, occurs near the resonator, the air in the resonator begins to sound loudly in its special tone. Other frequencies are "ignored" by this simple machine.
See the Helmholtz resonators bottle-form and bowl-form/ "Condom" form in his original work.
Here an example of amplifying tones of a big bell by gourd-like vessels on "Torre das Cabacas" in Santarém/ Portugal... other examples can be found in antique greek theaters...
If a combined sound has to be analyzed, Helmholtz-Resonators of different sizes are stuck into the ear. A resonance tone is heard always then, when the correspondent partial tone is included in the sound's tone mixture. The loudness of the tone thus heard corresponds to the loudness of the partial tones.
With that simple method, sound-analyses of amazing exactness (when compared with "modern" methods) were possible at the end of the 19th century.
Inevitably the question of computing will arise now...
The Resonance frequency (=Frequency of the flute)
In case of a round soundhole :
f = ((r x c)/2) x SQR[ 1 / (V x Pi x (d + (1,7 x r )))]
Irregular shape of the soundhole:
f = ( c / (2 x Pi)) x SQR[A / (V x ( d + SQR( A )))]
c = Velocity of sound in
cm/s
f = Frequency of the resonator in
Hz
d = Wall thickness of the resonator
at its opening in cm
r = Radius of the
soundhole in cm
V = Volume of the
resonators in cm3
A = Area
of the soundhole in cm2
Volume of the Resonator
In case of a round soundhole:
V = ((r2 x c2) / (4 x Pi x f2 x (d + SQR(A)))
Irregular shape of the soundhole:
V = (A x c2) / 4 x Pi2 x f2 x (d + SQR( A ))
c = Velocity of sound in cm/s
f
= Frequency of the resonator in Hz
d =
Wall thickness of the resonator at its opening in cm
r
= Radius of the soundhole in cm
V =
Volume of the resonators in cm3
A
= Area of the soundhole in cm2
Here's an online calculator for Helmholtz-resonators
For further details please see the pages by Dr. Godfried-Willem Raes (in Dutch).
Now, if you want to know the frequencies of the whistles in the kite hovering over you in the air, you just could take some Helmholtz-Resonators and measure easily....
The whistles need a minimum windspeed of about 5/sec and above. So, when you decide to build a windwheel with some flutes on its wingtips, you need a wheel-diameter of about 160cm provided a turning-frequency of 1Hz.
(see the very special string: The "Compound-String" of the Cambodian "Èk" or "Aik")
Vibrating strings are the twodimensional pendant to swinging membranes. Strings don't have a self-elasticity, therefore they must be fixed at their ends to be able to perform elastic oscillations at all. Of particular significance are bending oscillations (or transversal oscillations) which are used in stringed instruments. The strings can be vibrated by beating (piano, hammers), plucking (guitar), by bowing (violin) or rubbing (longitudinal; super long metal strings). The strings of Aeolian harps or kite musical bows are incited by the wind.
This mechanism can effet fatal damage to powerlines. See the super site on the "Galopping" Phänomenon - nothing else but a huge aeolian harp...
The exact mechanism HOW the wind forces a string to vibrate is well studied meanwhile. Vincenc Strouhal was the first, who made in 1878 his habilitation about the theme "Über eine besondere Art der Tonerregung" ("On a special way of generating tones"), where he described tone induction by an airstream blowing against wires or sharp edges. Playing an important role considering tone generation, the generation of vortices in the lee of the string is well illustrated by the following animation (Courtesy is the beautiful page of Cesareo de La Rosa Siqueira). These so called "Von Kármán Vortex Street" forces the string's vibrating by the rhythmic alternating detachment of vortices dependent on the string's diameter and the windspeed. These resonance phenomenons even caused the destruction of bridges (See video! 700K and explanation of the disaster) ... a flat string on a musical kite bow works in the same manner. In case of resonance between the vortex frequency and the string frequency (could be also a rod of metal or wood), a loud tone can be heard like in aeolian harps:
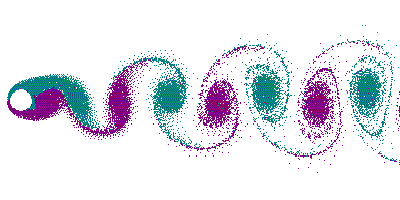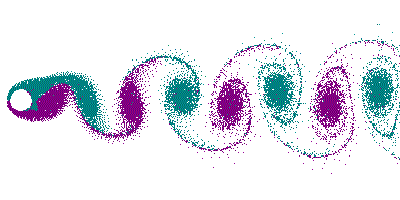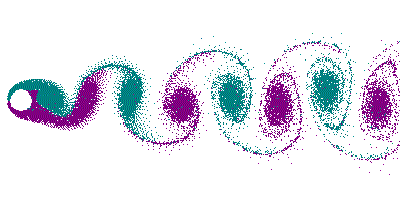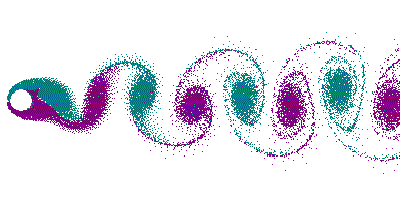
And that's the acoustic impression of such a Vortex Street... (die Aufnahme entstand an meiner Zimmertür als draußen ein Gewitter tobte...
Even in free nature the Kármán vortex streets (see
literature and his biography)
can be seen as clouds in the Lee
of Islands (Courtesy is the page of T.J.Praisner).
Or, the movement/ swinging of iced wires in arctic areas when the
windspeed was almost zero; see Alaska
Science Forum . All these phenomenons "work" after
the same principle (see some literature
about vortex induced tones).
See a very practical
experiment in the bathtub.
Another beautiful (!)
simulation of vortex streets at strings:
http://www.swcp.com/itsc/movies/acel.mpg
Back to the strings:
Round strings have a very
small projected area, which they can present to the wind for
being "vibrated". Therefore there are only very few kite
musical instruments with round strings (I only know the Chinese kite
hummer).
For improving the string's responding/sound radiation,
the projected area has to be enlarged. This is either made by
ribbon-shaped strings (examples are the Chinese Yao-Ch'in, the
Cambodian Èk, the Japanese Unari, the Chinese Fêng Chêng; see
instruments of the "Harp Type")
or a paper-vane is glued onto a part of a round string as it
is done with the Bermuda or the Russian kite hummer.
So, only a very low wind-speed is required to vibrate the string, generating a maximum effect....
When fixing several ribbon strung instruments on a kite, look out not to put them too near together! The strings make moving a considerable amount of air volume around them, disturbing other strings located too nearby in a negative manner. In extreme cases, the influenced string can stay completely mute at all. Its the same with vibrations, which are transmitted from one stringed instrument onto another by means of a holding apparatus.
When a string is plucked, it will swing as a whole in the beginning, thus generating the fundamental tone. But it will swing also in itself in a manner, that vibration-knots will always be at the fixed ends, thus producing overtones/ harmonics.
If l is the length of the string and c the velocity of the wave in the string (dependent on the string's tension), then will be valid for the frequency f :
f = n·c / 2·l with n = 1,2,3,...
For n = 1 is obtained the frequency f 0 of the fundamental oscillation:
f 0 = c / 2·l
The frequencies of the harmonic oscillations/ tones you will get, when inserting the numbers of 2, 3, 4,... . So its easily seen, that the frequencies of the harmonic tones (overtones) are entire multiples of the fundamental frequency.
The string generates harmonic tones and therefore an agreeable sound.
Swinging membranes or swinging poles being fixed at one side have both unharmonic overtones, i.e. no entire multiples of the fundamental tone. Therefore no agreeable sound can develop, but a tone mixture. So membranes and swinging plates are of only limited value for musical purposes.
General formula for the frequency v in dependence of the string's length l, the tension force K, the area F and the density of the string material p:
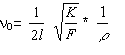
Or a little different the Taylor-formula, where f is the frequency, L the length, P the tension and m the mass per string unit:
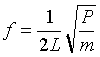
Here's another good article about the behaviour of strings. At the end, interesting remarks about aeolian tones.
Just a word to the relationship of the length of a string and its frequency. When a string length of 1 is given, generating the tone "C", the next tones of the octave (D, E, F...) can be found by multiplying the string length of 1 with the factors seen in the table below. These ratios are valid for all tones!
The table below shows the "temperate" tuning, a special way of tuning an instrument.
The tone a'=435,00Hz. (Determined by an international conference in Vienna in 1885.)
|
Length of string/ ratio |
1 |
8/9 |
4/5 |
3/4 |
2/3 |
3/5 |
8/15 |
1/2 |
|
Musical name |
C' |
D' |
E' |
F' |
G' |
A' |
H' |
C'' |
|
Frequency (Hz) |
261.63 |
293.66 |
329.63 |
349.23 |
392.00 |
440.00 |
493.88 |
523.25 |
According to Relf there is existing a borderline windspeed concerning the possibility of sound-generation by the wind at strings, represented by an empiric equation:
V*D/v
>=100
V = Wind-velocity, D = diameter of wire, v
= Viscosity of medium (air etc.)
When at a given diameter of the wire the result of the equation is lee than approx. 100, no vortex-street is generated, thus no sound.
And for mathematics-lazybones here's a link to a
calculation program for strings for downloading:
http://www.wadsworth-lutes.co.uk/software.htm
Special
feature:
Compound-String,
the Cambodian "Ek"
(Back to beginning of "Strings")
First, hear an example of the Cambodian "Ek"-Musical
Kite-Bow.
Please
note, all the different successive tones are
made by ONE SINGLE string only!! The "Èk"
doesn't produce a constant tone; the latter being the case with
the Japanese "Unari".
The
compound string, consisting of a middle, ribbon shaped part and
several thin threads on its both sides, which are fixed to the ends
of the bamboo-bow. In contrary to the "normal" strings
described above, that special type of string has a completely other
behaviour. It doesn' t have the "normal" longitudinal and
transversal vibrations but does alternating revolutions around its
lengthwise axis in different sense and speeds.
The tone
frequency, however, is determined by the identical revolution-cycle
frequency, which is determined by the number of "vibration
bellies". It depends on the string's moment of inertia. The
more weight and the more width of the string, the slower the movement
and the tone frequency will be. So, for making a deeper tone,
the Cambodians glue a bit of bee's wax to the ends of the middle
part of the string in order to increase the moment of inertia.
Besides of the rotation frequency (pitch of the tone is loudest around 4000Hz/cps for human ears) the projected area of the middle part of the string plays the main role for the loudness of the instrument. The bigger the radiating area, the louder the tone will be. So it is good, to build the instrument not too small...
For changing the length/ time of a single
rotation-cycle, other things play an important role too:
The
tension of the bow. The more tension, the shorter
the cycle AND the higher the pitch will be!
The torsion
resistance of the fixation-threads. The more resistance, the
shorter the cycle (single tone) will be.
As you can easily see on
an "Ek" in action, additionally to the rotating motion
there are also swinging-bulges/ knots on the string like on the flat,
non-rotating string of the japanese "Unari". Few bulges =
low pitch; many bulges = high pitch of the string. The tones of an
"Ek" don't change but are repeated in a random succession.
Beneath, have a look on a frequency analysis of an Èk.
There are 6 main peaks for the main tones. 7 tones are
considered the "non plus ultra"; as a "Well made bow"
in Cambodia .. The deep tones below 172Hz are the "switch
tones", when the string changes its revolving direction.
The
peaks have same distance from another , a sign for harmonic
tones, i.e the instrument doesn't produce dissonances.
|
|
Main-Frequencies of an "Èk". 6 Peaks
in equal distance. |
Strings, above all round ones, are normally bad acoustic
radiators. Musical instruments therefore have parts (boxes
etc.) which are forced to resonate/ vibrate with the tone, the
string is producing. Because of its great surface, the
resonant parts of an instrument act as a good "radiator" of
sound.
The PAPER KITE with its large, tough, (ideally)
paper covered frame is an IDEAL RESONANCE BODY !
Self-resonance shouldn't appear; if great amplitudes occur in case of a "resonance catastrophe" the kite is in theoretical danger to tear off, .
Further possibilities for amplifying is the combination of several flutes of the same tuning, a principle used with Chinese Nantong Kite Flutes and Cai-Sao, the "Weinheim Querflöte" and the "Wind Organ". (see there)
The main method for amplifying the string's tone in an aeolian harp is to adjust the resonance frequency of the instrument's body to the"main-tone" (=the tone mostly heard when the harp is playing). This resonance frequency is determined by the ratio of the resonance-body's volume and the size of its soundhole.Below, you can see the frequencies obtained by knocking against the soundboard of an Aeolian Harp. When the harmonics of the strings meet these tones, so these special tones appear with increased volume.
|
|
|
Knocking-Spectrum |
An important aspect of music, which is amusing to play with, are
the so called acoustic interference. That effect is produced
intentionally with the Nantong Kite Flutes and the "Wind Organ"
and is an essential part of their sound performance.
To produce an
acoustic interference two flutes are slightly "mistuned",
so that there is only little difference between their frequencies
(hear an example on
http://www.monroeinstitute.com/programs/bbapplet.html).
When
superpositioning of the two differing frequencies occurs, the result
is a vibration/ frequency, which is the arithmetic mean (f1+f2)/2
of the frequencies of the both partial oscillations. The amplitude
varies between zero and a maximum value with the frequency
fs=|f1-f2|.
For sound waves this will mean: When two sound waves of nearly the
same frequency meet, instead of the two tones with the
frequencies f1
and f2 only one
single tone with the frequency (f1+f2)/2
can be heard. The volume of the tone is swaying with the frequency fs
= |f1-f2|
between a maximum and a minimum value. When the amplitudes of both
sound waves are exactly the same, the minimal value=0 and the maximal
value will be double the amplitude of the single tone. In case of the
acoustic interference frequency fs
is higher than 16Hz (= low threshold of the human ear), no more
swaying can be heard but a independent tone.
By the way: Acoustic interferences are practically used when tuning an instrument. Two strings/ flutes are then tuned in exactly the same tone, when no more acoustic interference occurs, i.e.only one tone of constant volume can be heard when both strings are plucked simultaneously.
The so-called "Vox coelestis" of an church-organ is made that way, when there is no space or no money for the special (deep sounding) organ flute. So the required tone can be obtained, although the special (big) flute for this tone is physically NOT PRESENT!
Here is a nice site on sound interferences "beats" with sound examples: http://www.phys.unsw.edu.au/jw/beats.html
Just one word for the best time to make the kite musical instruments sound....
The best time is the night time by the following reasons:
Particularly in clear nights without clouds, the ground is quickly "radiating" into the space its warmth-energy accumulated during the day. The effect is, that the air-layer on the ground will become colder very fast (fog!) and the upper layers stay warmer. Under these circumstances a "beam of sound" which is sent inclined to the sky, will be reflected like by a mirror (refraction) and sent back again to the earth. In this case, the range of sound is extended very much. During the day the upper air-layers are colder than the ground-layers heated by the sun, the sound is refracted into the sky and the range thus will be shortened. See beautiful site on that theme...
In clear autumn-, winter- and spring nights without clouds the conditions are best for air flowing laminar like oil. Then, the cold air flowing down the mountain by night makes strings sounding wonderfully...
Provided that the air temperature will stay the same, the wind too can influence the way of a sound-beam. The sound running with the wind will be bent to the earth, the sound against the wind is bent into the sky. This is one reason why words being called against the wind can be heard on a very short distance only (apart from the noise generated by the wind itself). So the range of a sound signal can be influenced very strongly by the windspeed.
So, that's it.
All things as clear as daylight...? Hope you
understood my translation-efforts. It's hard stuff, really....
P.S. Don't miss A.Campanella's pages on acoustics - or do you know that there's something like sonoluminescence...?
For further reading: the books by Fletcher and Spektrum der Wissenschaft on physics of musical instruments.
New ideas, criticism, corrections......? Then please Mail to Kite Musical Instruments!
Want to see/ hear more? Then back to Kite/ Aeolian Musical Instruments Mainpage
This site was made and developed by
Uli Wahl, all
rights reserved